Belajar Python Principal Component Analysis (PCA)

Made Raditya Pujamurti - August 20, 2022

PCA adalah salah satu teknik yang paling populer untuk mengurangi dimensi independent variables. Kali ini kita akan cari tau cara implementasi PCA di Python dengan bantuan Scikit-Learn.

Masalah:

Terlalu banyak independent variables atau features di dataset yang kita punya. Akurasi model jadi rendah karena curse of dimensionality.

Solusi:

Bisa pakai Principal Component Analysis (PCA).

Seperti biasa import library dulu.

import numpy as np
from sklearn.decomposition import PCA
from sklearn import datasets
import matplotlib.pyplot as plt

Kita pake data yang populer dari Scikit-Learn: Wine dataset

wine_data = datasets.load_wine()
wine_data.feature_names

['alcohol',
 'malic_acid',
 'ash',
 'alcalinity_of_ash',
 'magnesium',
 'total_phenols',
 'flavanoids',
 'nonflavanoid_phenols',
 'proanthocyanins',
 'color_intensity',
 'hue',
 'od280/od315_of_diluted_wines',
 'proline']

Ada banyak fitur yang ada untuk sebuah wine, seperti yang bisa dilihat di atas.

Kita juga bisa lihat berapa banyak fitur dari independent variables dengan cara ini:

X = wine_data.data
y = wine_data.target
X.shape

(178, 13)

Mungkin ada bagusnya buat tau korelasi antara setiap feature:

cov = np.corrcoef(X.T)
cov

array([[ 1.        ,  0.09439694,  0.2115446 , -0.31023514,  0.27079823,
         0.28910112,  0.23681493, -0.15592947,  0.13669791,  0.5463642 ,
        -0.0717472 ,  0.07234319,  0.64372004],
       [ 0.09439694,  1.        ,  0.16404547,  0.2885004 , -0.0545751 ,
        -0.335167  , -0.41100659,  0.29297713, -0.22074619,  0.24898534,
        -0.56129569, -0.36871043, -0.19201056],
       [ 0.2115446 ,  0.16404547,  1.        ,  0.44336719,  0.28658669,
         0.12897954,  0.11507728,  0.18623045,  0.00965194,  0.25888726,
        -0.07466689,  0.00391123,  0.22362626],
       [-0.31023514,  0.2885004 ,  0.44336719,  1.        , -0.08333309,
        -0.32111332, -0.35136986,  0.36192172, -0.19732684,  0.01873198,
        -0.27395522, -0.27676855, -0.44059693],
       [ 0.27079823, -0.0545751 ,  0.28658669, -0.08333309,  1.        ,
         0.21440123,  0.19578377, -0.25629405,  0.23644061,  0.19995001,
         0.0553982 ,  0.06600394,  0.39335085],
       [ 0.28910112, -0.335167  ,  0.12897954, -0.32111332,  0.21440123,
         1.        ,  0.8645635 , -0.4499353 ,  0.61241308, -0.05513642,
         0.43368134,  0.69994936,  0.49811488],
       [ 0.23681493, -0.41100659,  0.11507728, -0.35136986,  0.19578377,
         0.8645635 ,  1.        , -0.53789961,  0.65269177, -0.1723794 ,
         0.54347857,  0.7871939 ,  0.49419313],
       [-0.15592947,  0.29297713,  0.18623045,  0.36192172, -0.25629405,
        -0.4499353 , -0.53789961,  1.        , -0.3658451 ,  0.13905701,
        -0.26263963, -0.5032696 , -0.31138519],
       [ 0.13669791, -0.22074619,  0.00965194, -0.19732684,  0.23644061,
         0.61241308,  0.65269177, -0.3658451 ,  1.        , -0.02524993,
         0.29554425,  0.5190671 ,  0.3304167 ],
       [ 0.5463642 ,  0.24898534,  0.25888726,  0.01873198,  0.19995001,
        -0.05513642, -0.1723794 ,  0.13905701, -0.02524993,  1.        ,
        -0.52181319, -0.42881494,  0.31610011],
       [-0.0717472 , -0.56129569, -0.07466689, -0.27395522,  0.0553982 ,
         0.43368134,  0.54347857, -0.26263963,  0.29554425, -0.52181319,
         1.        ,  0.56546829,  0.23618345],
       [ 0.07234319, -0.36871043,  0.00391123, -0.27676855,  0.06600394,
         0.69994936,  0.7871939 , -0.5032696 ,  0.5190671 , -0.42881494,
         0.56546829,  1.        ,  0.31276108],
       [ 0.64372004, -0.19201056,  0.22362626, -0.44059693,  0.39335085,
         0.49811488,  0.49419313, -0.31138519,  0.3304167 ,  0.31610011,
         0.23618345,  0.31276108,  1.        ]])

Waduh output nya kegedean. Kalo gitu bisa kita coba pake chart heatmap:

img = plt.matshow(cov, cmap=plt.cm.Reds)
plt.colorbar(img, ticks=[-1, 0, 1])

<matplotlib.colorbar.Colorbar at 0x292fec91e48>

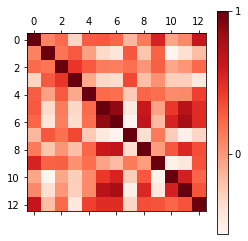
Oke ada beberapa fitur yang punya korelasi tinggi. Akan lebih simpel kalo kita bisa cuma dapetin 2 independent variables dari sekian banyak features ini.

Salah satu caranya bisa pakai Principal Component Analysis (PCA):

pca_2 = PCA(n_components=2)
X_pca_2 = pca_2.fit_transform(X)
X_pca_2.shape

(178, 2)

Setelah ditransformasi dengan PCA, jumlah fiturnya jadi tinggal 2. Mantapp! 👍

pca_2.explained_variance_ratio_.sum()

0.9998271461166032

Jumlah informasi yang masih tersimpan di 2 komponen ini pun masih tinggi (lebih dari 95%).

Sekarang kita bisa coba bikin chart untuk liat persebaran kategori wine, dengan principal component sebagai axis/sumbu chart:

plt.scatter(X_pca_2[:, 0], X_pca_2[:, 1], c=y)
plt.show()

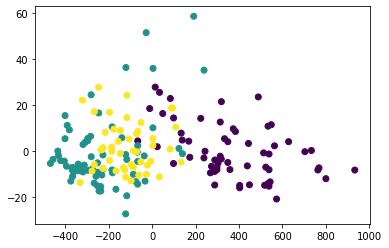
Kita udah berhasil punya 2 fitur untuk mewakili semua independent variables yang ada.

Tapi masih kurang jelas perbedaan antara kelompok wine 1 dan yang lain. Untuk masalah ini ada topik lain yaitu tentang scaling yang kita akan bahas nanti.