Deteksi Outlier Dengan Python

Made Raditya Pujamurti - November 6, 2022

Masalah:

Perlu deteksi outlier secara otomatis.

Solusi:

Bisa coba pakai scaling terus cari nilai yang diluar kelipatan standard deviation tertentu atau pakai EllipticEnvelope dari ScikitLearn

import numpy as np
from sklearn import datasets
from sklearn import preprocessing
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.covariance import EllipticEnvelope

Kita coba dengan toy data breast cancer.

cancer_data = datasets.load_breast_cancer()
cancer_data.data[0]

array([1.799e+01, 1.038e+01, 1.228e+02, 1.001e+03, 1.184e-01, 2.776e-01,
       3.001e-01, 1.471e-01, 2.419e-01, 7.871e-02, 1.095e+00, 9.053e-01,
       8.589e+00, 1.534e+02, 6.399e-03, 4.904e-02, 5.373e-02, 1.587e-02,
       3.003e-02, 6.193e-03, 2.538e+01, 1.733e+01, 1.846e+02, 2.019e+03,
       1.622e-01, 6.656e-01, 7.119e-01, 2.654e-01, 4.601e-01, 1.189e-01])

Salah satu cara untuk deteksi outlier dengan otomatis adalah dengan ngasi batas nilai standard deviation setelah scaling. Jadi nilai yang di atas standard deviation tertentu bisa dianggap menyimpang terlalu jauh makanya dikasi label sebagai outlier.

Berikut ini cara untuk scaling datanya.

features_normalized = preprocessing.StandardScaler().fit_transform(cancer_data.data)
features_normalized[0]

array([ 1.09706398, -2.07333501,  1.26993369,  0.9843749 ,  1.56846633,
        3.28351467,  2.65287398,  2.53247522,  2.21751501,  2.25574689,
        2.48973393, -0.56526506,  2.83303087,  2.48757756, -0.21400165,
        1.31686157,  0.72402616,  0.66081994,  1.14875667,  0.90708308,
        1.88668963, -1.35929347,  2.30360062,  2.00123749,  1.30768627,
        2.61666502,  2.10952635,  2.29607613,  2.75062224,  1.93701461])

Sekarang tinggal tentuin batas nilai dan di kasus ini kita pakai 3 standard deviation buat jadi limit nya.

Kita bisa print daftar titik mana aja yang masuk kategori outlier. Metode zip() sederhananya bakal bikin pasangan untuk setiap baris(row) dan kolom nya.

outlier_row, outlier_column = np.where(np.abs(features_normalized) > 3)
print(list(zip(outlier_row, outlier_column)))

[(0, 5), (3, 4), (3, 5), (3, 9), (3, 18), (3, 24), (3, 25), (3, 28), (3, 29), (9, 25), (9, 26), (9, 29), (12, 11), (12, 12), (12, 15), (12, 17), (12, 19), (14, 25), (14, 29), (23, 23), (25, 8), (31, 28), (31, 29), (35, 28), (42, 15), (42, 18), (42, 25), (60, 8), (68, 15), (68, 16), (68, 17), (68, 26), (71, 9), (71, 14), (71, 15), (71, 19), (72, 25), (78, 5), (78, 6), (78, 8), (78, 18), (78, 28), (82, 0), (82, 2), (82, 3), (82, 5), (82, 6), (82, 7), (82, 22), (83, 11), (105, 4), (105, 29), (108, 5), (108, 6), (108, 7), (108, 12), (108, 15), (108, 26), (112, 16), (112, 19), (116, 14), (119, 18), (119, 28), (122, 2), (122, 3), (122, 4), (122, 5), (122, 6), (122, 7), (122, 8), (122, 10), (122, 11), (122, 12), (122, 13), (122, 14), (122, 15), (122, 16), (122, 18), (138, 10), (138, 18), (146, 8), (146, 18), (146, 28), (151, 19), (151, 29), (152, 6), (152, 9), (152, 15), (152, 16), (152, 17), (152, 19), (176, 15), (176, 19), (180, 0), (180, 2), (180, 3), (180, 7), (180, 20), (180, 22), (180, 23), (181, 5), (181, 25), (190, 15), (190, 18), (190, 25), (190, 28), (190, 29), (192, 11), (202, 6), (203, 24), (212, 0), (212, 2), (212, 3), (212, 10), (212, 12), (212, 13), (212, 18), (213, 14), (213, 15), (213, 16), (213, 17), (213, 19), (219, 1), (219, 21), (232, 1), (236, 20), (236, 23), (239, 1), (239, 21), (258, 5), (258, 10), (258, 12), (259, 1), (259, 21), (265, 13), (265, 20), (265, 21), (265, 22), (265, 23), (288, 15), (288, 17), (290, 15), (290, 19), (314, 14), (314, 18), (318, 9), (323, 28), (339, 3), (339, 23), (345, 14), (351, 18), (352, 0), (352, 2), (352, 3), (352, 6), (352, 7), (352, 20), (352, 22), (352, 23), (368, 13), (368, 23), (370, 28), (376, 9), (376, 16), (376, 19), (379, 24), (379, 25), (379, 29), (388, 19), (389, 17), (400, 26), (416, 11), (417, 10), (417, 12), (430, 26), (461, 0), (461, 2), (461, 3), (461, 6), (461, 7), (461, 10), (461, 12), (461, 13), (461, 20), (461, 22), (461, 23), (473, 11), (503, 10), (503, 12), (503, 13), (503, 20), (503, 22), (503, 23), (504, 4), (504, 9), (505, 9), (505, 14), (521, 2), (521, 3), (521, 23), (557, 11), (559, 11), (561, 11), (562, 25), (562, 26), (562, 29), (567, 5), (567, 6), (567, 25), (567, 26), (568, 4)]

Tapi karena ada lebih dari 2 fitur, bakal susah buat visualisasinya. Jadi kita bisa pake PCA buat ngurangin dimensi/fitur nya jadi 2.

pca_2 = PCA(n_components=2)
X_pca_2 = pca_2.fit_transform(features_normalized)
X_pca_2.shape

(569, 2)

Dari kompenen PCA ini kita bisa filter lagi baris dan kolom mana yang nilainya lebih dari 3 standar deviasi. Filter ini ada di metode np.where(np.abs(X_pca_2) > 3)

pca_outlier_row, pca_outlier_column = np.where(np.abs(X_pca_2) > 3)
print(list(zip(pca_outlier_row, pca_outlier_column)))

[(0, 0), (1, 1), (2, 0), (3, 0), (3, 1), (4, 0), (5, 1), (8, 0), (8, 1), (9, 0), (9, 1), (12, 0), (14, 0), (14, 1), (15, 0), (17, 0), (18, 0), (18, 1), (21, 0), (22, 0), (22, 1), (23, 0), (23, 1), (24, 0), (25, 0), (26, 0), (27, 0), (28, 0), (30, 0), (31, 1), (32, 0), (33, 0), (37, 0), (38, 1), (42, 0), (45, 0), (46, 0), (50, 0), (51, 0), (52, 0), (53, 0), (56, 0), (58, 0), (59, 0), (61, 1), (62, 0), (62, 1), (63, 1), (67, 0), (68, 0), (68, 1), (69, 0), (70, 1), (71, 1), (72, 0), (77, 0), (78, 0), (78, 1), (82, 0), (83, 0), (85, 0), (87, 0), (95, 0), (97, 0), (101, 0), (101, 1), (102, 0), (105, 0), (105, 1), (107, 0), (108, 0), (112, 0), (112, 1), (113, 1), (114, 1), (116, 1), (117, 0), (118, 0), (121, 0), (122, 0), (125, 0), (127, 1), (129, 0), (137, 0), (138, 0), (140, 0), (144, 0), (145, 1), (146, 1), (149, 0), (151, 1), (152, 0), (152, 1), (153, 0), (156, 0), (157, 1), (158, 0), (159, 0), (161, 0), (162, 0), (164, 0), (164, 1), (166, 0), (168, 0), (173, 0), (174, 0), (175, 0), (176, 1), (178, 0), (178, 1), (179, 0), (180, 0), (180, 1), (181, 0), (185, 0), (186, 1), (188, 0), (189, 0), (190, 0), (190, 1), (192, 0), (198, 0), (202, 0), (203, 0), (203, 1), (206, 0), (210, 0), (210, 1), (212, 0), (212, 1), (213, 0), (218, 0), (219, 0), (219, 1), (226, 0), (229, 1), (230, 0), (231, 0), (232, 0), (233, 0), (233, 1), (234, 0), (236, 0), (236, 1), (237, 1), (239, 0), (241, 0), (242, 1), (244, 0), (246, 0), (250, 0), (251, 0), (252, 0), (254, 0), (256, 0), (257, 0), (257, 1), (258, 0), (258, 1), (259, 0), (260, 0), (260, 1), (261, 1), (262, 0), (263, 1), (265, 0), (265, 1), (269, 1), (270, 0), (270, 1), (271, 0), (272, 0), (272, 1), (273, 0), (274, 1), (276, 0), (277, 1), (278, 0), (280, 0), (282, 0), (285, 0), (287, 0), (288, 1), (289, 0), (290, 0), (290, 1), (294, 0), (295, 0), (296, 0), (299, 0), (300, 0), (302, 0), (303, 0), (304, 0), (305, 0), (306, 0), (307, 0), (308, 0), (308, 1), (309, 0), (310, 0), (311, 0), (311, 1), (313, 0), (314, 0), (314, 1), (315, 0), (316, 0), (318, 1), (319, 0), (320, 1), (321, 1), (323, 0), (324, 0), (326, 0), (327, 0), (332, 0), (333, 0), (334, 0), (335, 0), (337, 0), (338, 0), (339, 0), (339, 1), (343, 0), (345, 1), (346, 0), (348, 0), (350, 0), (351, 0), (351, 1), (352, 0), (352, 1), (354, 0), (357, 0), (359, 0), (360, 0), (364, 0), (365, 1), (366, 0), (368, 0), (368, 1), (369, 0), (369, 1), (370, 0), (372, 0), (373, 0), (373, 1), (376, 1), (377, 0), (379, 0), (379, 1), (381, 0), (387, 0), (388, 1), (389, 0), (390, 0), (391, 0), (392, 0), (393, 0), (398, 0), (400, 0), (401, 0), (404, 0), (412, 0), (417, 0), (419, 0), (425, 0), (428, 0), (429, 0), (430, 0), (430, 1), (432, 0), (433, 0), (439, 0), (442, 0), (443, 0), (446, 0), (449, 0), (449, 1), (458, 0), (459, 0), (460, 0), (461, 0), (461, 1), (467, 0), (468, 0), (469, 1), (473, 0), (477, 0), (479, 0), (485, 1), (487, 0), (491, 1), (492, 0), (493, 0), (498, 0), (499, 0), (501, 1), (503, 0), (503, 1), (504, 1), (505, 1), (507, 1), (509, 0), (517, 0), (520, 1), (521, 0), (521, 1), (522, 0), (524, 0), (525, 0), (527, 0), (533, 0), (535, 0), (537, 1), (538, 0), (539, 1), (546, 0), (548, 0), (550, 0), (553, 0), (556, 0), (557, 0), (561, 0), (562, 0), (562, 1), (563, 0), (564, 0), (564, 1), (565, 0), (565, 1), (567, 0), (568, 0)]

Buat ditampilin di graph nanti, kita juga bisa cari data yang termasuk normal alias bukan outlier.

pca_normal_row, pca_normal_column = np.where(np.abs(X_pca_2) < 3)

Sekarang kita coba tampilin graph secara keseluruhan.

plt.scatter(X_pca_2[:, 0], X_pca_2[:, 1], c=cancer_data.target)
plt.show()

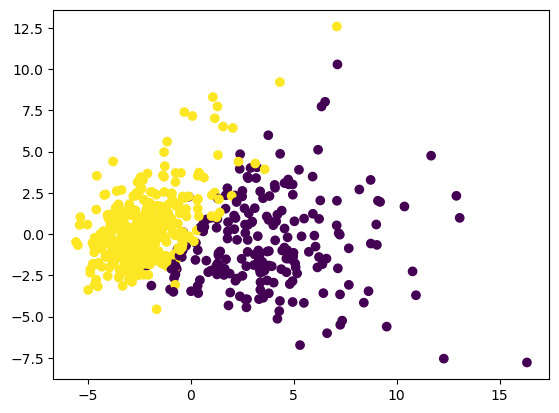
Terus bandingin dengan grafik yang cuma nampilin data yang bukan outlier.

normal = plt.plot(X_pca_2[pca_normal_row, 0], X_pca_2[pca_normal_row, 1], 'x', color='green', alpha=0.7, label='normal')

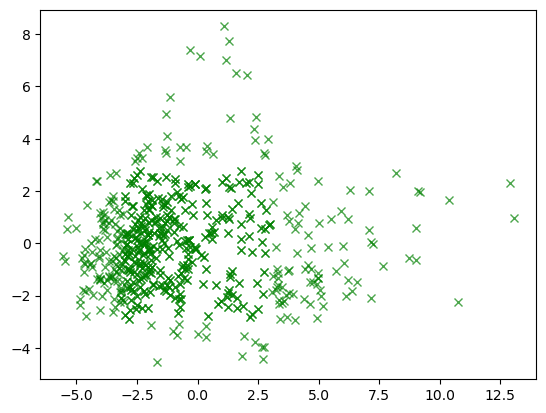
Kalo yang cuma outlier bakal seperti ini.

outliers = plt.plot(X_pca_2[pca_outlier_row, 0], X_pca_2[pca_outlier_row, 1], 'o', color='red', alpha=0.7, label='outliers')

Atau kita juga bisa gabungin kedua grafik sebelumnya biar lebih gampang ngeliatnya.

normal = plt.plot(X_pca_2[pca_normal_row, 0], X_pca_2[pca_normal_row, 1], 'o', color='green', alpha=0.7, label='normal')
outliers = plt.plot(X_pca_2[pca_outlier_row, 0], X_pca_2[pca_outlier_row, 1], '+', color='red', alpha=0.7, label='outliers')
plt.legend((normal[0], outliers[0]), ('normal', 'outliers'), numpoints=1, loc='upper right')
plt.show()

Sepertinya hasil di atas kurang bagus dan kita mau coba cara lain.

Function lain yang kita bisa coba adalah EllipticEnvelope. Satu parameter penting di sini adalah contamination yang simpelnya berapa persen dari total data adalah outlier. Jadi semakin besar nilai contamination, jumlah data yang dikategorikan jadi outlier bakal makin banyak.

elliptic_cov = EllipticEnvelope(contamination=0.05).fit(X_pca_2)
detected_outliers = elliptic_cov.predict(X_pca_2)
np.unique( detected_outliers)

array([-1,  1])

Bisa diliat EllipticEnvelope() bakal ngasi prediksi dengan nilai -1 (outlier) atau 1 (bukan outlier).

Dan kita bisa pilah datanya dengan cara ini:

elliptic_normal_row = np.where(detected_outliers==1)
elliptic_outliers_row = np.where(detected_outliers==-1)

Sekarang kita bisa pake cara yang mirip dengan sebelumnya buat nampilin chart.

normal = plt.plot(X_pca_2[elliptic_normal_row, 0], X_pca_2[elliptic_normal_row, 1], 'o', color='green', alpha=0.7, label='normal')
outliers = plt.plot(X_pca_2[elliptic_outliers_row, 0], X_pca_2[elliptic_outliers_row, 1], '+', color='red', alpha=0.7, label='outliers')
plt.legend((normal[0], outliers[0]), ('normal', 'outliers'), numpoints=1, loc='upper right')
plt.show()

Buat eksperimen, coba ganti nilai contamination=0.01 dan liat perbedaanya.

elliptic_cov = EllipticEnvelope(contamination=0.01).fit(X_pca_2)
detected_outliers = elliptic_cov.predict(X_pca_2)
detected_outliers[0]
elliptic_normal_row = np.where(detected_outliers==1)
elliptic_outliers_row = np.where(detected_outliers==-1)
normal = plt.plot(X_pca_2[elliptic_normal_row, 0], X_pca_2[elliptic_normal_row, 1], 'o', color='green', alpha=0.7, label='normal')
outliers = plt.plot(X_pca_2[elliptic_outliers_row, 0], X_pca_2[elliptic_outliers_row, 1], '+', color='red', alpha=0.7, label='outliers')
plt.legend((normal[0], outliers[0]), ('normal', 'outliers'), numpoints=1, loc='upper right')
plt.show()

Bisa diliat jumlah outlier jadi makin sedikit dan nilai contamination ini tergantung skenario masing-masing. Teman-teman bisa baca lebih lanjut tentang EllipticEnvelope() di dokumentasi resminya.

Semoga bermanfaat!